Application Notes : kSA 400 – Growth Rate Method
Version: 1.0
- 1. Introduction
- 2. Growth Rate using Fourier Transforms
- 3. Growth Rate Via Damped Sine Wave Analysis
- 4. Growth Rate Extrema Count Analysis
- 5. Comparing Results of All Three Methods
1. Introduction
The kSA 400 analytical RHEED system has evolved over the past twelve years into an extremely powerful quantitative surface analysis system. The kSA 400 (V4.30 and higher) has three separate analysis routines for determining growth rate from RHEED intensity oscillations.1
These routines are:
1) Fast-Fourier Transform (FFT)
2) Damped Sine Wave Fit, and
3) Extrema Count analysis.
Because each routine uses completely different analysis algorithms, they yield completely independent methods for determining growth rate. Hence, they can be compared with one another for consistency.
1.1 Scan Mode Images and *.kdt Files
Most users perform kSA 400 Growth Rate Analysis Routines on data acquired through Scan Mode. Scan Mode generates two types of data files: *.kdt files and Scan Mode images. A *.kdt file contains all the intensity information from the user-defined regions. For example, in Figure 2, four regions have been defined for data monitoring and acquisition. The resulting *.kdt file data can be displayed as a chart, which allows for manipulation and plotting of all data from the regions stored in the file: see Figure 3 below. Of course, growth rate may be extracted from any or all of the regions.
Scan Mode images are generated by stacking successive line profiles – each beneath the previous one. This yields images which show how the line profile evolved over time. In Figure 4, on the next page, the Scan Mode image was created from a single line scan through the specular beam. As shown in the image, intensity oscillations are decreasing with time because more material is deposited. Growth rate information can be extracted from both *.kdt files and Scan Mode images. The sections below detail the process of extracting growth rates by the kSA 400’s three methods.
1For a review of the principles of RHEED intensity oscillations, refer to P.J. Dobson et al, “Current Understanding and Applications of the RHEED Intensity Oscillation Technique”, J. of Crys. Growth 81 (1987), pp. 1-8.
2. Growth Rate using Fourier Transforms
The most common method for determining growth rate is using Fourier transforms (FFT and DFT). Fourier transforms take a time-dependent data set (the RHEED oscillation data) and turn it into a data set with a frequency domain, regenerating this data set by adding all frequency components, (i.e. sine and cosine waves of all frequencies) to generate the original frequency-dependent data. The frequency component with the largest amplitude is the peak frequency, i.e., the growth frequency. To perform Growth Rate FFT on a Scan Mode Image, select the image and select Intensity Oscillations from the Analysis menu. A red rectangle appears on the image. Position the rectangle over the vertical streak (an example of the streak is in Figure 4). Then right-click the intensity oscillations window and select the Data tab: choose peak, minimum, centroid, average, or center intensity. For the most accurate analysis, Fourier transform only the oscillation data and not any static data before growth started. To do so, select a subset of the data by placing the mouse cursor at the left limit of the plot, then right-clicking and selecting “Set X Min.”
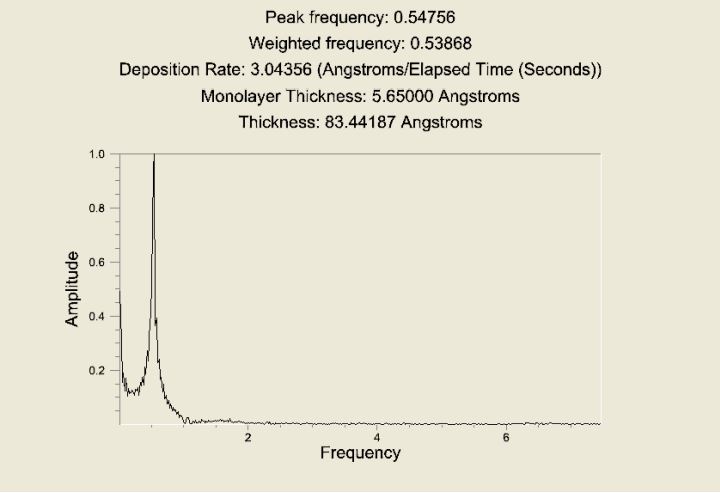
Next, select Growth Rate FFT from the Analysis menu. A new window pops up with the FFT data displayed, as shown in Figure 5 below. The routine plots the power spectrum of the Fourier transform as a function of frequency. The peak in the plot shows the peak frequency of the oscillations. The sharper the peak, the cleaner and more constant the oscillations are.
The title of the plot lists several calculated values, including peak frequency, deposition rate, and total thickness. Thickness is calculated from peak frequency, monolayer thickness, and the time interval in the data set.
Figure 5: Intensity oscillations data set and corresponding FFT analysis.
The following section describes how to adjust the parameters for the FFT analysis routine.
2.1 Growth Rate FFT Fitting Parameters.
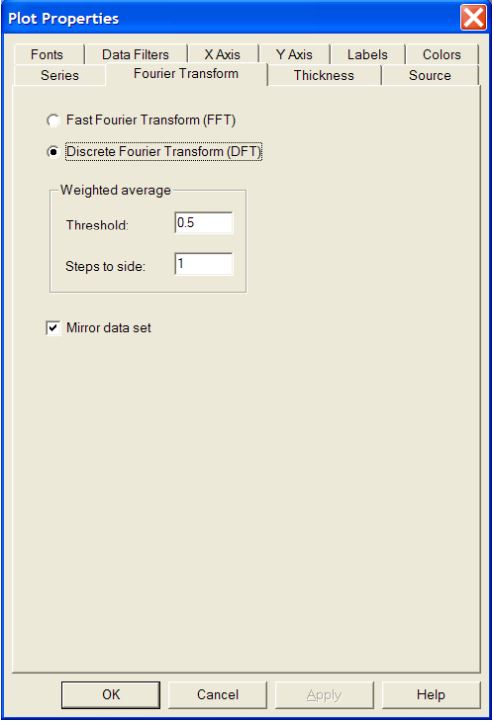
In order to modify the parameters for the FFT analysis, right click on the FFT chart and select Properties from the drop down menu. From the Properties dialog select the Fourier Transform tab, as shown in Figure 6 below.
2.1.1 Fourier Transform Tab Parameters
FFT vs. DFT. While very fast, the Fast Fourier Transform (FFT) algorithm may introduce numerical error into the calculation. This is because FFT requires data sets that are a power of two in length. Zeros are added to data sets to get the proper length, and this can lead to small errors in determining the frequency. The Discrete Fourier Transform (DFT) does not have this deficiency. Unless the data set is very large data set (or a very slow computer), we recommend using the Discrete Fourier Transform (DFT) for analysis. While slower, DFT provides more accurate analysis of the frequency.
Weighted average. The weighted average frequency takes the shape of the power spectrum peak frequency into account, and calculates a weighted average frequency based on this shape. If the peak frequency profile is perfectly symmetric, then the weighted average frequency and the peak frequency are identical. This calculation uses Threshold and Steps to side parameters.
Threshold. This parameter sets the height of the peak profile below which a weighted average is not calculated. For example, a threshold of .5 means that the weighted average is calculated for the top 50% of the peak profile. The threshold value is useful, for example, for eliminating asymmetries in the peak profile.
Steps to side. This parameter sets the number of data points to each side of the peak that are used in the weighted average calculation. For example, a value of 1 means that the weighted average algorithm will take 1 data point to each side of the peak (as long as they are
above the threshold value).
Mirror data set. Check this option to mirror the intensity data set about itself, thereby doubling the number of data points fed into the Fourier transform. In most cases selecting Mirror data set will yield a cleaner Fourier transform, but in some cases you will get some additional harmonics that may result in an erroneous peak. The best way to check this is to first disable this checkbox, look at the peak frequency, and then turn on Mirror data set. The new peak should be within 5% of the old one.
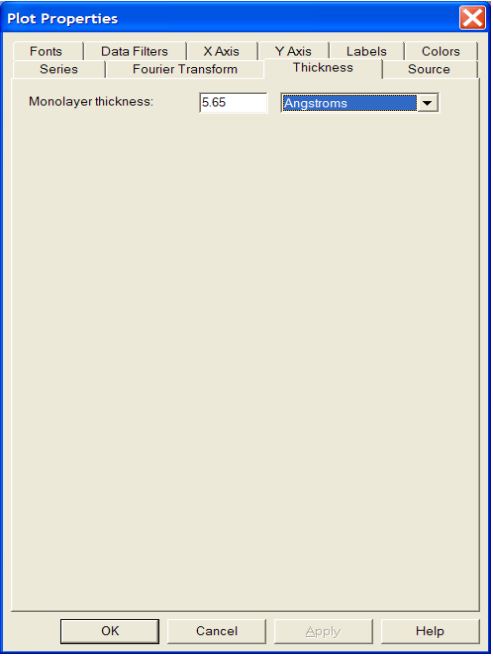
2.1.2 Thickness Tab Parameters
The Thickness Tab allows you to enter the monolayer thickness for the material deposited. For example, for GaAs, the monolayer thickness is 5.65 A. The thickness can be entered in either angstroms or nanometers. The dialog is shown below. Note similar dialogs are present as well for the other two growth rate methods.
2.2 Helpful Hints When Using the Growth Rate FFT Analysis
When analyzing intensity oscillation data, there are a multitude of intensities that can be analyzed: peak intensity, average intensity, centroid intensity, etc. If oscillations are very strong, then analyzing the peak intensity is usually sufficient. However, if there is noise or the oscillations are weak, then typically the average intensity data is the best data to analyze. Furthermore, because peak intensity may saturate at some point during acquisition, average intensity usually does not and so is still valid data for growth rate determination.
Finally, note that boxcar smoothing the intensity oscillation data may also yield cleaner Fourier transform analysis. To perform boxcar smoothing, right-click the intensity oscillation chart, selecting Properties. Then select the Data Filters tab, and then select the Boxcar smooth filter. Click the Properties… button to select the smooth width. Applying the Boxcar smooth filter smoothes out the noise from oscillation data. Running Growth Rate Fourier transform analysis on the smoothed data may yield a sharper Fourier transform.
3. Growth Rate Via Damped Sine Wave Analysis
Most RHEED oscillation data fit a damped sine wave function very well. This method for determining growth rate fits the data using the following equation:
![]()
- w = intensity oscillation frequency (units of Hz)
- a0 = amplitude (units of intensity)
- a1 = envelope coefficient (units of Hz)
- a2 = phase offset (units of radians)
- a3 = offset (units of intensity)
- a4 = offset damping coefficient (units of Hz)
The parameter w is the oscillation frequency; hence w yields the deposition rate. Also of interest is a1, the envelope coefficient. a1 is essentially a measure of how rapidly the oscillations are decaying: a large value for a1 means a rapid decay, which generally indicates a rapidly roughening surface. A small value for a1 generally indicates that the surface is roughening at a slower rate. a2, the phase offset, can be compared between different diffraction streaks. Each diffraction streak has a different phase of oscillation, although the frequency of oscillation will be the same.
The kSA 400 fits the damped sine wave equation to the supplied data set by using a gradient-expansion algorithm to compute a non-linear least squares fit. This routine requires input of the partial derivatives of the original function, which are known exactly. The algorithm iterates until the chi-squared values only slightly vary, or until 1000 iterations are performed without convergence.
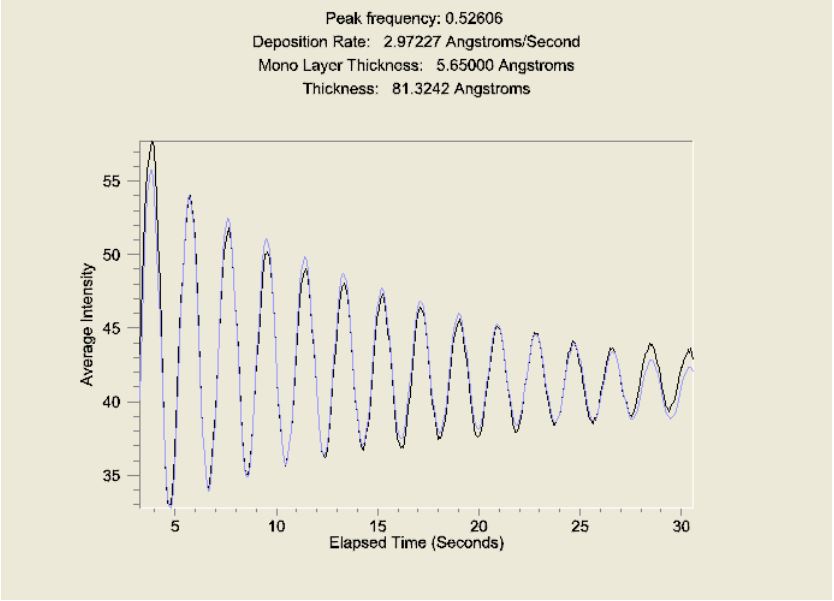
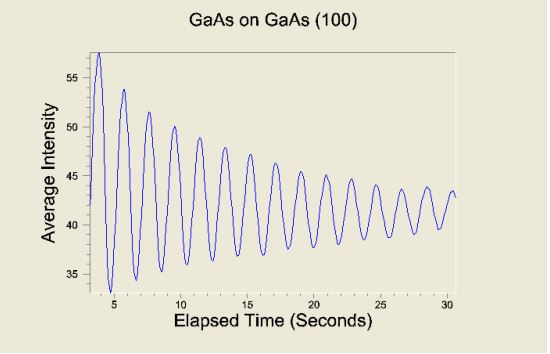
A typical data set from Intensity Oscillations analysis and fit is shown below:
Figure 8: Growth Rate Damped Sine Fit analysis showing original oscillation data (black) and fit data (blue).
In order to perform the Growth Rate Damped Sine Fit, first select the subset of data for fitting. Selecting a subset of the data is easily done by placing the mouse cursor at each limit on the plot, then right-clicking and selecting “Set X Min/Max” from the pop-up dialog. Then select Growth Rate Damped Sine Fit from the Analysis menu. In general, the fit will not converge until reasonable estimates are made for the fitting parameters. This is discussed in the following section.
3.1 Fitting Parameters and Estimates
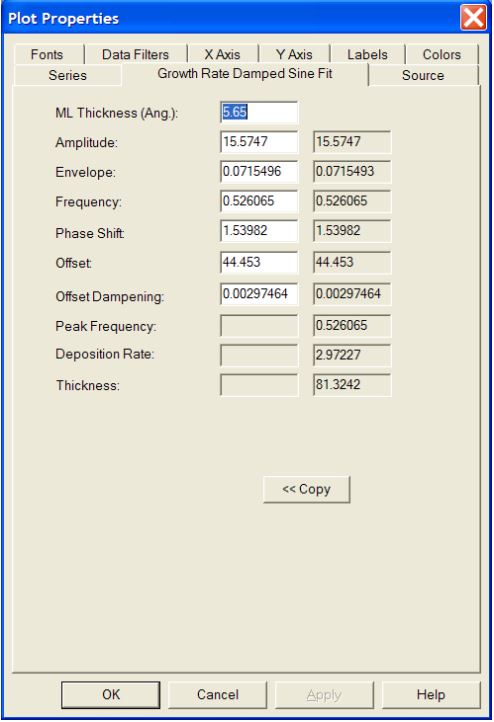
Right-click the Growth Rate Damped Sine Wave Fit window (even if no fit was made due to lack of convergence) and select Properties. Then select the Growth Rate Damped Sine Fit tab in order to see the dialog shown in Figure 9.
The parameters listed within this dialog are the same parameters listed in Section 3 above. In order to converge, reasonable estimates for the parameters must be input. Proper values for the fit in Figure 8 are shown in the corresponding dialog of Figure 9. Estimate the parameters in the following way:
Amplitude. The amplitude is the average peak to valley distance, in units of intensity. This can be a little tricky to estimate for heavily damped oscillations, but only a rough estimate is needed. Envelope. This is the envelope coefficient, and can always be estimated at 0.001. The correct value will be determined by the system upon convergence.
Frequency. This is the oscillation frequency. This can be estimated by first doing a Growth Rate FFT analysis on the data, or can be estimated by looking at the time difference between peaks and taking the inverse of the change in time, Δt .
Phase shift. Always estimate the phase shift to be zero. The correct value will be determined upon convergence.
Offset. The offset is the average value of the oscillations, i.e., the mid-point or mid-intensity of the oscillations. This is the offset from zero.
Offset damping. Always estimate the offset damping coefficient to be 0.001. The correct value will be determined by the system upon convergence.
<<Copy. This button copies the fitting parameters determined by the fit to the current input parameters. Once you get convergence, generally you will want to copy the exact fit parameters over to the input parameters for use with the next fit.
3.2 Helpful Hints For Using the Growth Rate Damped Sine Fit Analysis.
The key to using the Growth Rate Damped Sine Fit algorithm is providing it with reasonable estimates. The most important parameters to estimate are the frequency, offset, and amplitude. Also, while this algorithm is not as sensitive to noise as the Fourier transform algorithm, smoothing the data with a boxcar smooth may yield slightly better fits.
Finally, note that it is always useful to compare the results of the various methods. You can run all three growth rate analysis routines on the same source data, and can compare results side-by-side.
4. Growth Rate Extrema Count Analysis
The Growth Rate Extrema Count method first calculates the first derivative of the intensity data set and finds the zero crossings in the derivative data, i.e., it determines the extrema in the intensity data. Then the algorithm determines a set of frequencies from the intervals between the zero crossings. The average of these frequencies yields the final growth rate frequency.
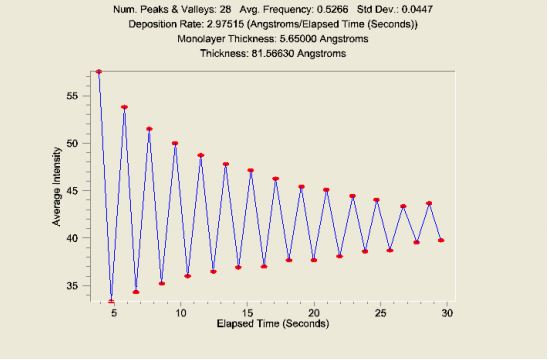
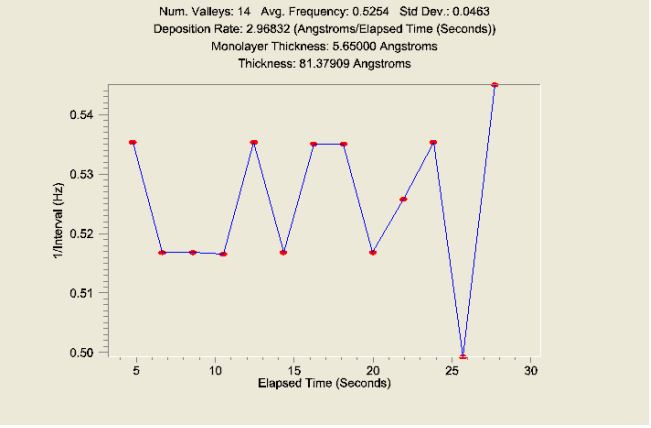
To perform Growth Rate Extrema Count analysis, first select the oscillation data set you want to analyze. Selecting a subset of the data is easily done by placing the mouse cursor at each limit on the plot, then right-clicking and selecting “Set X Min/Max” from the pop-up dialog. Then select Growth Rate Extrema Count from the Analysis menu. As an example, the data set from Intensity Oscillations analysis and its extrema count analysis are shown in Figure 10, where red markers are placed on the extremas.
4.1 Growth Rate Extrema Count Fitting Parameters
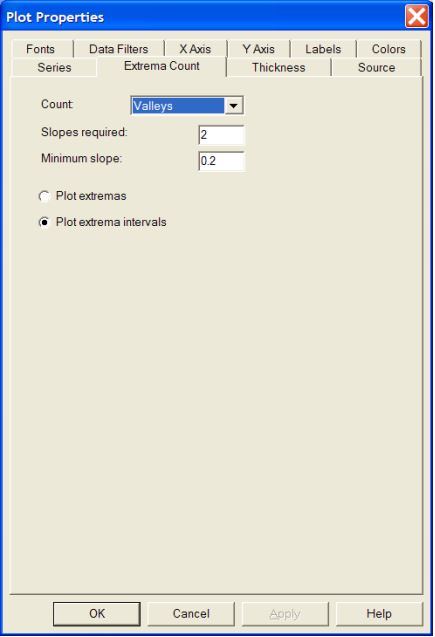
In order to adjust the extrema count fitting parameters, right click on the extrema count plot and select Properties, then select the Extrema Count tab from the Properties dialog, as shown in Figure 11 below. The parameters within this dialog are explained below.
Count. This dropdown box allows you to select which type of extrema you want to count: peaks, valleys, or peaks and valleys. If your data has strong oscillations like that shown here, then selecting peaks and valleys will yield the most accurate growth rate analysis.
Slopes required. This parameter allows fine tuning of what is considered a peak and what is considered noise. For example, setting Slopes required to 2 means for each peak found there must be two positive slopes in succession immediately to the left of the peak, and two negative slopes in succession immediately to the right of the peak. Otherwise the peak is considered. Note that using boxcar smoothing can reduce noise and eliminate erroneous peaks.
Minimum slope. This parameter allows you to select the minimum slope deemed a real slope about a peak. The units are in intensity per unit time. The default value of 0.2 is generally good for most oscillation data.
Plot extremas/intervals. This radio button switches the plot from one of extrema values, as shown above in Figure 10, to one of the intervals between extremas, as shown in Figure 12 on the next page. The usefulness of the interval plot, which effectively plots the growth rate as a function of time, is that it shows the growth transients during deposition. Note however that as the oscillations become weaker and harder to resolve, the extrema to extrema growth rate calculation becomes less accurate. As a result, “transients” like those shown in the last two data points of Figure 12 may not really be transients, but noise in the analysis.
4.2 Helpful Hints When Using the Extrema Count Analysis
Noise in the intensity data affects extrema analysis. As a result, we recommend always boxcar smoothing the intensity data before running the extrema count analysis on it. This is easily done by right-clicking on the intensity oscillation chart, selecting Properties, then selecting the Data Filters tab, then the Boxcar smooth data filter. Increase the number of data points in the smooth by clicking the Properties… button and adjusting the smooth number.
5. Comparing Results of All Three Methods
It is simple to compare the growth rate numbers from all three methods simultaneously: select the intensity oscillation data that you want to analyze, set the X Min/Max values, and then run all three analyses on the data by selecting the analysis type from the Analysis menu. In this way you can compare results directly from all three methods.